Пример INPUT.TXT:
0 0
0 2
3 0
3 2

OUTPUT.TXT для примера:
6

Найти рациональное решение уравнения с точностью 1/1000. Решением является несократимая дробь p/q (p,q - натуральные числа), такая что .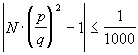

Во входном файле в первой строке содержится целое число N (2 ≤ N ≤ 1000).

В выходной файл вывести решение в виде p/q.

Пример INPUT.TXT:
9

OUTPUT.TXT для примера:
1/3

Фирма "Му-му" решила поздравить своих клиентов с Международным днем трудящихся, но дворник Герасим, посланный на почту, все перепутал и взял конверты трех типов, несоответствующие по размерам и количеству открыткам тоже трех типов. Требуется разложить открытки по конвертам и отправить их. Открытки нельзя сгибать, класть под углом (стороны открытки должны быть параллельны сторонам конверта), отправлять без конверта. Какое максимальное число клиентов сможет поздравить фирма?

Во входном файле содержится шесть строк. В первых трех строках содержится информация о трех типах конвертов, в следующих трех строках – информация о трех типах открыток. В каждой строке содержится три натуральных числа N_i, A_i, B_i через один пробел. N_i – количество конвертов или открыток (1 ≤ N_{i ≤} 100), A_i и B_i – размеры в миллиметрах (0<B_{i ≤} A_{i ≤} 1000).

Пример INPUT.TXT:
2 100 75
3 120 60
2 100 70
6 100 80
8 100 75
9 110 60

OUTPUT.TXT для примера:
5

В предыдущей задаче запрещалось класть открытку в конверт под углом, но если это разрешить, тогда, например, в конверт 90x90 можно положить открытку 20x100. Написать программу, которая по размерам конверта и открытки позволяет определить, можно ли положить открытку в конверт, не сгибая.

Во входном файле содержится две строки. В первой строке указаны два натуральных числа A и B через пробел (1 ≤ A,B ≤ 1000) – размеры открытки в миллиметрах. Во второй строке указаны два натуральных числа C и D через пробел (1 ≤ C,D ≤ 1000) – размеры конверта в миллиметрах.

Пример INPUT.TXT:
20 100
90 90

OUTPUT.TXT для примера:
YES

На доске имеется три колышка A, B и C. На колышек A нанизаны N одинаковых дисков, пронумерованных сверху вниз от 1 до N. Колышки B и C пустые. Необходимо перенести все диски на колышек B, используя в качестве вспомогательного колышек C и соблюдая следующие правила :

1. нельзя возвращать диски на колышек A;
2. нельзя снимать диски с колышка B;
3. можно перемещать только по одному диску за ход.

Определить, возможно ли получить заданный конечный порядок размещения дисков на колышке B и минимальное количество ходов для этого.

Во входном файле в первой строке содержится количество дисков N (1 ≤ N ≤ 1000) на колышке A. Следующие N строк файла содержат перестановку чисел от 1 до N (по одному числу в строке) – требуемое расположение дисков на колышке B в порядке сверху вниз.

В выходной файл вывести минимальное число ходов, если возможно получить указанное конечное расположение дисков, соблюдая правила, или 0 (ноль), в противном случае.

Пример INPUT.TXT:
6
2
3
4
5
6
1

OUTPUT.TXT для примера:
10